27.02.21

Die Fibonacci-Zahlenfolge Design und Proportion – eine Spirale weist den Weg
Leonardo Fibonacci
Vor rund 800 Jahren lernte der Italiener Leonardo Pisano (1170-1240), besser bekannt als Leonardo Fibonacci bei seinen Reisen um das Mittelmeer die gesamte damalige Mathematik. Er schrieb das Buch „Liber Abaci“. Mit dessen Hilfe verbreitete er im 13. Jahrhundert das heutige indisch-arabische Zahlensystem in Europa. In diesem Buch wird erstmals auf die Fibonacci-Zahlenfolge hingewiesen. Er hat die Fortpflanzungsrate von Kaninchen und das besondere Geheimnis des Wachstumsprozesses in der Natur berechnet. In Bildsprache wird die Fibonacci-Folge als Spirale dargestellt – die Goldene Spirale.

Die Berechnung der Harmonie
Die Fibonacci-Reihe folgt einer einfachen Gesetzmäßigkeit. Jede Zahl ist die Summe der zwei vorangegangenen Zahlen. Deren Ursprung liegt bei 1. Das Zahlenwachstum nimmt im Verlauf der Reihe immer mehr zu. Die Zahlen werden schnell größer.
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
55 + 89 = 144
Wie konstruierst du mit den Fibonacci-Zahlen die Goldene Spirale?
Als Konstruktionsgrundlage dient ein Raster aus aneinander gereihten Quadraten mit der Seitenlänge der Fibonacci-Zahlen. Die in den Quadraten entstehenden Kreissegmente verbinden sich zur Fibonacci-Spirale. Diese öffnet sich immer weiter, da das Zahlenwachstum schnell zunimmt. Hier lässt sich mit etwas Fantasie die Verbindung zur Natur herstellen. Siehst du die Schnecke?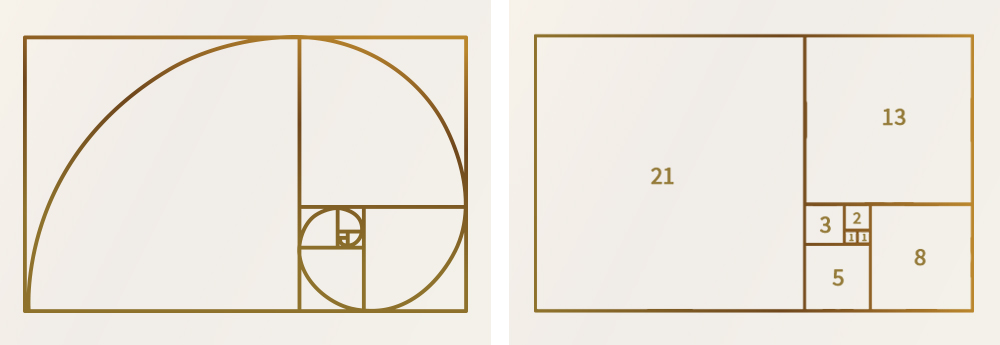
Die Fibonacci-Zahlen und der Goldene Schnitt sind verwandt
Vereinfachen wir das Raster aus dem vorangegangenen Bild, ergeben sich ein Quadrat und ein Rechteck. Diese Flächenaufteilung entspricht nahezu dem Goldenen Schnitt.

Der Goldene Schnitt bezeichnet das Verhältnis von zwei Flächen oder zwei Teilstrecken zueinander. Dabei verhält sich der größere zum kleineren Teil ebenso wie das Ganze zum größeren Teil. Dafür steht in der Mathematik die Phi-Zahl 1.618.
Wie wird der Goldene Schnitt konstruiert?
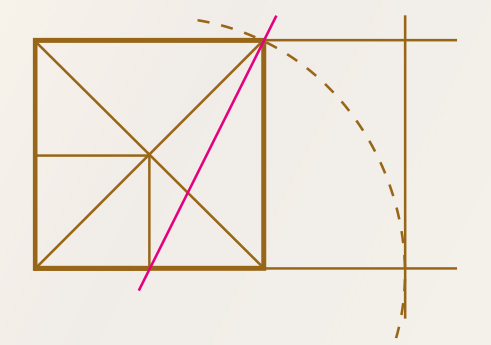
Um eine Fläche im Goldenen Schnitt zu teilen, schau dir folgendes Beispiel an. Es gibt natürlich noch viele mehr.
Wofür nutzen wir die Fibonacci-Zahlen und den Goldenen Schnitt?
Fibonacci-Reihe
Die Fibonacci-Reihe entspringt demselben Grundsatz wie der Goldene Schnitt. Beide beschreiben Wachstumsprozesse in der Natur. Betrachte beispielsweise die links- und rechtsdrehenden Spiralen eines Kiefernzapfen, eines Kaktus oder einer Sonnenblume. Sie stehen im Verhältnis von 8 zu 13 oder 21 zu 34 auf (Zahlen der Fibonacci-Reihe).

Jeder einzelne Sonnenblumenkern gehört zu einer linksdrehenden und zu einer rechtsdrehenden Spirale. Die Anzahl der Spiralen sind allesamt benachbarte Zahlen aus der Fibonacci-Zahlenfolge.
In der Sonnenblume ergeben sich immer Spiralenkombinationen von 21/34, 34/55, 55/89 und in großen Sonnenblumen auch 89/144 Kernen.
Teilst du diese Zahlen durcheinander, so ist das Ergebnis immer 1,618, („Phi“ bzw. Goldener Schnitt).
Goldener Schnitt
Schon in der Antike galten Proportionen denen der Goldene Schnitt zu Grunde lagt als schön und ästhetisch. Er ergibt sich aus der Gleichheit der Proportionen. Überall, wo es um Proportionen und eine harmonische Aufteilungen geht, greifen wir auf diese Berechnungen zurück.
Am bekanntesten ist dabei der Satzspiegel. So wird die konstruierte Seitenaufteilung bei Büchern, Broschüren und Zeitschriften genannt. Alle möglichen Abstände und Größen für Seitenränder, Spaltenabstände oder Zeilenabstände werden auf der Grundlage dieser Formeln berechnet. Dabei geht es um das Verhältnis der bedruckten Fläche zum Weißraum.
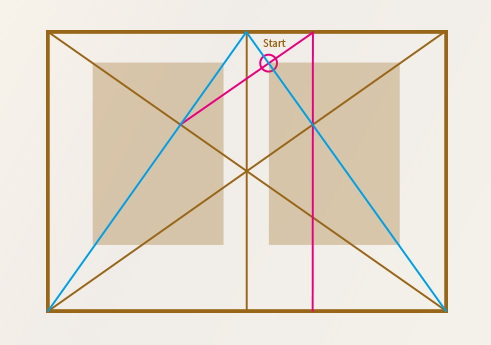
Auch in der Fotografie und in der Malerei kannst du durch die Anwendung dieser Gestaltungsgrundlagen auf die Bildaufteilung und -komposition die Bildwirkung beeinflussen.

Beispiel: Legst du dein Hauptmotiv genau auf das innere der Spirale, erhält dein Bild eine harmonische und ausgewogene Wirkung.